Structured Query Language (SQL)
What is Structured Query Language (SQL)?
Structured Query Language (SQL) is a standardized programming language that is used to manage relational databases and perform various operations on the data in them. Initially created in the 1970s, SQL is regularly used not only by database administrators but also by developers writing data integration scripts and data analysts looking to set up and run analytical queries.
The term SQL is pronounced ess-kew-ell or sequel.
SQL is used for the following:
- Modifying database table and index structures.
- Adding, updating and deleting rows of data.
- Retrieving subsets of information from within relational database management systems (RDBMSes). This information can be used for transaction processing, analytics applications and other applications that require communicating with a relational database.
SQL queries and other operations take the form of commands written as statements and are aggregated into programs that enable users to add, modify or retrieve data from database tables.
A table is the most basic unit of a database and consists of rows and columns of data. A single table holds records, and each record is stored in a row of the table. Tables are the most used type of database objects or structures that hold or reference data in a relational database. Other types of database objects include the following:
- Views are logical representations of data assembled from one or more database tables.
- Indexes are lookup tables that help speed up database lookup functions.
- Reports consist of data retrieved from one or more tables, usually a subset of that data that is selected based on search criteria.
Each column in a table corresponds to a category of data -- for example, customer name or address -- while each row contains a data value for the intersecting column.
How do relational databases work?
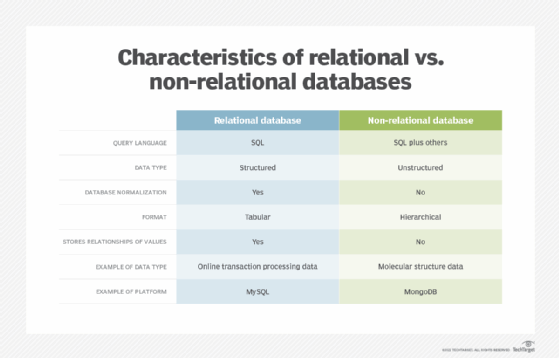
Relational databases are relational because they are composed of tables that relate to each other. Non-relational databases, on the other hand, don't use rows and tables, but instead use data models such as key-value pairs, graphs and column families to store and organize data.
Relational databases use a tabular layout to store information, with rows and columns representing different data qualities and the various relationships between the data values. For example, a SQL database used for customer service can have one table for customer names and addresses and other tables that hold information about specific purchases, product codes and customer contacts. A table used to track customer contacts usually uses a unique customer identifier called a key or primary key to reference the customer's record in a separate table used to store customer data, such as name and contact information.
SQL became the de facto standard programming language for relational databases after they emerged in the late 1970s and early 1980s.
Why is SQL important?
SQL is a great language to learn because it's the primary database language used for data processing tasks and is used across various industries.
The following reasons highlight the importance of SQL:
- Backbone of the data industry. SQL is considered the backbone of the data industry. It's widely used by data-centric professionals including data analysts, data scientists, business analysts and database developers.
- Universal language. SQL is a universal language that is transferable to other disciplines and languages. Learning SQL can help one understand the workings of other languages such as Python and Java. It also makes collaboration easy, as it has a large supportive community.
- In-demand skill. SQL knowledge is one of the most in-demand skills in the field of data science. It appears in a significant percentage of data science job postings, making it a prized skill for professionals in this field.
- Data manipulation. SQL is well-suited for data manipulation. It enables users to easily test and manipulate data, making it efficient for tasks such as filtering, sorting and aggregating data.
- Rapid query processing. SQL enables rapid query processing, enabling users to retrieve, manipulate or store data quickly and efficiently. However, optimizing queries for rapid processing involves a combination of proper indexing, query optimization and database design considerations.
- Security features. SQL provides various security features such as authentication, access control, audit trails and encryption, making it easy to manage permissions and ensure the security of data.
- Commonality and compatibility. SQL is widely used in various IT systems and is compatible with multiple other languages. Its commonality benefits beginners in the profession, as they are likely to use SQL throughout their careers. It also contributes to ease of application and improves the production and efficiency of businesses.
- Scalability. SQL is suitable for organizations of any size. It can easily scale up to accommodate future growth, making it a versatile choice for small and large businesses alike.
- Open source and community support. SQL is an open source language with a vibrant community of developers that regularly provide updates and troubleshooting assistance to SQL users.
- Cost-effective. Due to its open source nature, SQL is more cost-effective than proprietary solutions, making it ideal for organizations with budget constraints.
SQL standard and proprietary extensions
An official SQL standard was adopted by the American National Standards Institute (ANSI) in 1986, with the International Organization for Standardization (ISO) adopting the standard in 1987. New versions of the SQL standard are published every few years, the most recent in 2022.
ISO/IEC 9075 is the ISO SQL standard developed jointly by ISO and the International Electrotechnical Commission. The standard way of referring to an ISO standard version is to use the standards organizations -- ISO/IEC -- followed by the ISO standard number, a colon and the publication year. The current ISO standard for SQL is ISO/IEC 9075:2022.
Both proprietary and open source RDBMSes built around SQL are available for use by organizations. SQL-compliant database server products include the following:
- Microsoft SQL Server.
- Oracle Database.
- IBM Db2.
- SAP HANA.
- SAP Adaptive Server.
- Oracle MySQL.
- Open source PostgreSQL.
- Azure SQL Database.
- Google Cloud SQL.
Some versions of SQL include proprietary extensions to the standard language for procedural programming and other functions. For example, Microsoft offers a set of extensions called Transact-SQL, while Oracle's extended version of the standard is Procedural Language for SQL. Commercial vendors offer proprietary extensions to differentiate their product offerings by giving customers additional features and functions. As a result, the different variants of extended SQL offered by vendors are not fully compatible with one another.
SQL commands and syntax
SQL is, fundamentally, a programming language designed for accessing, modifying and extracting information from relational databases. As a programming language, SQL has commands and a syntax for issuing those commands.
SQL commands are divided into several different types, including the following:
- Data Definition Language (DDL) commands are also called data definition commands because they are used to define data tables.
- Data Manipulation Language (DML) commands are used to manipulate data in existing tables by adding, changing or removing data. Unlike DDL commands that define how data is stored, DML commands operate in the tables defined with DDL commands.
- Data Query Language consists of just one command, SELECT, used to get specific data from tables. This command is sometimes grouped with the DML commands.
- Data Control Language commands are used to grant or revoke user access privileges.
- Transaction Control Language commands are used to change the state of some data -- for example, to COMMIT transaction changes or to ROLLBACK transaction changes.
SQL syntax, the set of rules for how SQL statements are written and formatted, is similar to other programming languages. Some components of SQL syntax include the following.
- SQL statements start with a SQL command and end with a semicolon (;), for example:
SELECT * FROM customers;This SELECT statement extracts all of the contents of a table called customers.
- SQL statements are case-insensitive, meaning they can be written using lowercase, uppercase or a combination. However, it is customary to write out SQL keywords -- commands or control operators -- in all-caps and table/column names in lowercase. Words in the statement can be treated as case-sensitive using quotes, so the following two statements produce identical results.
SELECT * FROM customers;
select * from CUSTOMERS;These two statements are different:
SELECT * FROM customers;
SELECT * FROM "Customers";- SQL statements are terminated only by the semicolon, meaning that more complex statements can be rendered across multiple lines, like this one:
SELECT name, telephone, age
FROM customers;This command selects the contents of the columns name, telephone and age in the table customers.
- SQL statements can incorporate program flow controls, meaning that a statement can incorporate table and row selection -- as in the previous example -- and then operate on the data contained in those columns. For example, the following command selects the name, telephone number and birthdate for all customers whose age is over 21:
SELECT name, telephone, age
FROM customers
WHERE age > 21;Most SQL implementations include support for issuing statements at the command line, through a graphical user interface, by using SQL programs, or through application programming interfaces to access SQL databases using other programming languages.
Commonly used SQL commands with examples
Most SQL commands are used with operators to modify or reduce the scope of data operated on by the statement. Some commonly used SQL commands, along with examples of SQL statements using those commands include the following:
SQL SELECT. The SELECT command is used to get some or all data in a table. SELECT can be used with operators to narrow down the amount of data selected.
SELECT title, author, pub_date
FROM catalog
WHERE pub_date = 2021;This example could be used by a publisher to select the title, author and publication date columns from a table named catalog.
SQL CREATE. The CREATE command is used to create a new SQL database or SQL table. Most versions of SQL create a new database by creating a new directory, in which tables and other database objects are stored as files.
The following CREATE DATABASE statement creates a new SQL database named Human_Resources:
CREATE DATABASE Human_Resources;The CREATE TABLE command is used to create a table in SQL. The following statement creates a table named Employees that has three columns: employee_ID, last_name and first_name, with the first column storing integer (int) data and the other columns storing variable character data of type varchar and a maximum of 255 characters.
CREATE TABLE Employees (
employee_ID int,
last_name varchar(255),
first_name varchar(255)
);SQL DELETE. The DELETE command removes rows from a named table. In this example, all records of employees with the last name Smithee are deleted:
DELETE FROM Employees WHERE last_name='Smithee';This delete statement returns the number of rows deleted when it finishes running.
SQL INSERT INTO. The INSERT INTO command is used to add records into a database table. The following statement adds a new record into the Employees table:
INSERT INTO Employees (
last_name,
first_name
)
VALUES (
'Alan',
'Smithee'
);SQL UPDATE. The UPDATE command is used to make changes to rows or records in a specific table. For example, the following update statement updates all records that include a last_name value of Smithee by changing the name to Smith:
UPDATE Employees
SET last_name = 'Smith',
WHERE last_name = 'Smithee';SQL statements can use loops, variables and other components of a programming language to update records based on different criteria.
SQL-on-Hadoop tools
SQL-on-Hadoop query engines are a newer offshoot of SQL that enable organizations with big data architectures built around Hadoop data stores to use SQL as a querying language and let database professionals use a familiar query language instead of having to use more complex and less familiar languages -- in particular, the MapReduce programming environment for developing batch processing applications. These tools are designed to bridge the gap between SQL and Hadoop, enabling programmers and analysts to utilize their existing SQL expertise to query and analyze data stored in Hadoop.
More than a dozen SQL-on-Hadoop tools are available from Hadoop distribution providers and other vendors; many of them are open source software or commercial versions. In addition, the Apache Spark processing engine, which is often used in conjunction with Hadoop, includes a Spark SQL module that similarly supports SQL-based programming.
Not all SQL-on-Hadoop tools support all of the functionality offered in relational implementations of SQL. But SQL-on-Hadoop tools are a regular component of Hadoop deployments, as companies look to get developers and data analysts with SQL skills involved in programming big data applications.
Common SQL-on-Hadoop tools include the following:
- Apache Hive. It's a data warehouse infrastructure built on top of Hadoop that lets users query data stored on Hadoop Distributed File System (HDFS) using the Apache Hive Query Language. Hive is similar to SQL in the sense that both are query languages and both support data manipulation operations, data analysis and the concept of schemas, tables, rows and columns.
- Impala. Impala is an open source SQL query engine for Hadoop. It offers interactive, real-time SQL queries on data stored in the HDFS. Impala offers a broad range of SQL operations and is built for high-performance analytics.
- Presto. Presto is an open source big data distributed SQL query engine. Relational databases, NoSQL databases and Hadoop are just a few of the data sources from which it can query data. Presto is renowned for supporting ANSI SQL syntax and for executing queries quickly.
- Apache Drill. This is an open source SQL query engine that is compatible with several data sources, such as Hadoop, NoSQL databases and cloud storage. It enables sophisticated queries on structured and semistructured data and offers a schema-free SQL query interface.
- HAWQ. HAWQ is a SQL-on-Hadoop utility developed by Pivotal. It offers a fully functional SQL interface for accessing data stored in Hadoop and is built on top of the PostgreSQL database. HAWQ interacts with well-known business intelligence (BI) products and enables sophisticated SQL functionality.
- Jethro. Jethro is a commercial SQL-on-Hadoop engine that markets itself as the quickest for workloads related to BI. It offers fast SQL queries for Hadoop data and is compatible with a range of BI tools and programs.
SQL security
SQL servers are subject to most of the same vulnerabilities as any other enterprise application, including weak authentication, insecure design, misconfiguration and other application security issues. However, SQL injection, first reported in 1998, continues to dominate security issues for SQL systems.
The following are the common SQL security threats and their causes.
SQL injection attacks
SQL injection attacks usually exploit weaknesses in database systems where data submissions are not scanned and sanitized to remove potentially malicious code incorporated or injected into data.
The best-known example of a SQL injection exploit is documented in the "Little Bobby Tables" comic by Randall Munroe, in which a SQL injection is perpetrated by a mom who filled out a SQL form with her son's name followed by malicious SQL code.
In the comic, the son's name is entered as the following:
Robert'); DROP TABLE Students; --Following the valid data (Robert), the name continues with characters that SQL servers interpret as ending the data -- single quote, close parenthesis and semicolon -- followed by the DROP TABLE command.
Verbose errors
SQL Server databases can sometimes produce error messages containing internal information, potentially aiding attackers in identifying vulnerabilities or strategizing an attack.
It's imperative to ensure that all procedural code incorporates proper error handling mechanisms, thereby averting the exposure of default error messages to the user.
Privilege escalation
Privilege escalation attacks in SQL Server databases involve unauthorized attempts to elevate user privileges, enabling individuals to access data or execute functions beyond their designated level of authority.
To mitigate privilege escalation attacks, it's important to enforce preventative measures. These can include strict access controls, adhering to the principle of least privilege, regularly updating and patching the SQL Server software and conducting thorough security assessments to identify and address potential weaknesses.
Denial of service (DoS) attacks
In production environments, SQL Server databases often face the risk of application-layer DoS attacks, involving the flooding of fake queries by attackers. This slows down performance for legitimate users, leading to eventual downtime.
When using SQL Server in the cloud, one can utilize DoS protection services to detect and redirect malicious traffic, safeguarding the database from potential disruptions.
Lack of encryption
If a database or the data it contains is not encrypted properly, hackers can identify the points of connection between the machine and the network, which could result in database intrusions.
To lessen these risks, database administrators must maintain encryption for both the primary and backup SQL databases.
The use of best practices for database security can help protect an organization's most valuable digital assets. SQL security is an ongoing process and it's important to stay updated with the latest security practices and measures and conduct security audits to identify and address any new vulnerabilities.
History of SQL
With roots going back to the early 1970s, SQL continues to make key milestones as one of the most successful ideas in computing history.
The following is a timeline of the SQL language and its key milestones:
- 1970. "A Relational Model of Data for Large Shared Data Banks" by E.F. Codd is published in Communications of the ACM, laying the basis for RDBMSes.
- 1974. IBM researchers publish an article introducing Structured Query Language, first called SEQUEL or Structured English Query Language. The name was changed for trademark purposes.
- 1977. Relational Software Inc., the company that eventually became Oracle, begins building a commercial RDBMS.
- 1979. Oracle ships the first commercially available RDBMS for Digital Equipment Corp.'s minicomputer systems.
- 1982. IBM ships SQL/Data System, a SQL RDBMS for IBM mainframes.
- 1985. IBM ships Database 2, a SQL RDBMS for IBM's Multiple Virtual Storage mainframe operating system.
- 1986. An ANSI committee and then ISO adopt SQL as a standard.
- 1989. The first revision of the ISO SQL standard, SQL-89, is published.
- 1992. The first major revision of the ISQ SQL standard, SQL-92, is published.
- 1999. The first version to be named in accordance with ISO naming standards, ISO/IEC SQL:1999, adds programming functionality and support for Java.
- 2003. ISO/IEC SQL:2003 adds support for a predefined data type for Extensible Markup Language (XML) objects.
- 2006. ISO/IEC SQL:2006 expands XML-related functionality.
- 2008. ISO/IEC SQL:2008 adds support for partitioned JOINs, a method for linking two or more tables that treats the joined tables as a single table.
- 2011. ISO/IEC SQL:2011 improves support for relational databases containing time-related data.
- 2016. ISO/IEC SQL:2016 adds optional new features, including JavaScript Object Notation-related changes, support for polymorphic table functions and row pattern matching.
- 2017. ISO/IEC SQL:2017. SQL Server 2017 provides choices of development languages, data types, on-premises cloud and OS systems by adding the SQL Server power to Linux, Windows and Linux-based containers.
- 2019. ISO/IEC SQL:2019. SQL Server 2019 introduces Big Data Clusters for SQL and also offers additional options and improvements for the SQL Server database engine, SQL Server Analysis Services, SQL Server Machine Learning Services, SQL Server on Linux and SQL Server Master Data Services.
- 2022. ISO/IEC SQL:2022. SQL Server 2022 continues to build on the previous versions and their capabilities with additional features such as Azure Synapse Link, which is a real-time analytics feature, as well as enhanced security through features such as Microsoft Defender.
SQL skills and related careers
SQL skills can boost many careers, not just those of database administrators, data warehouse architects, database programmers and others whose roles directly use SQL.
Some other roles that can benefit from SQL experience include the following:
- Data scientists working with thousands of tables spread across thousands of databases need strong SQL skills.
- Business intelligence analysts must have strong SQL skills for working with data warehouses and structured databases.
- Data analysts are expected to have experience with SQL as they frequently perform tasks such as data retrieval, data manipulation, data cleaning and transformation.
- Cloud engineers are expected to be proficient in SQL, as cloud-based applications frequently rely on databases.
- Software developers benefit from having SQL skills, especially when working with databases, retrieving and manipulating data and building applications that rely on database functionality.
- Data engineers work on maintaining data pipelines and are expected to use SQL skills to extract, transform and load data from various sources into data warehouses or data lakes.
SQL skills can be helpful in a surprisingly broad range of disciplines. For example, journalists who reported in 2013 on offshore tax dodgers and money laundering had to learn SQL to help them understand the significance of the millions of emails and files that were leaked.
NoSQL systems are becoming more prevalent in the cloud, with numerous cloud providers and vendors offering them. Learn about the various types of NoSQL databases and their pros and cons.







